just-data

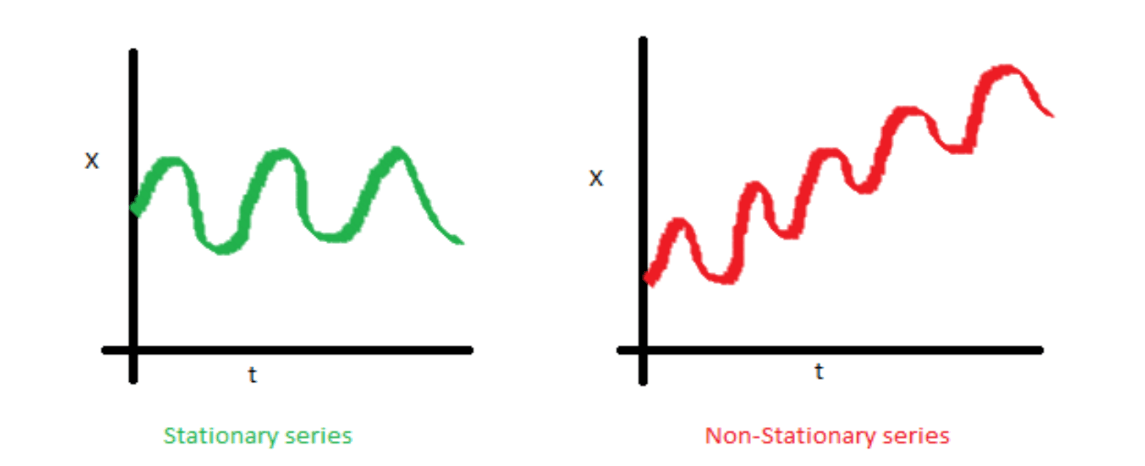
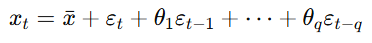본 글에서는 여러가지 시계열 모형의 구성과 개념, 그리고 모델 선택 방법을 정리해보도록 하겠습니다. 정상 시계열 모형AR(p) (Auto-Regressive Model)자기회귀(AR) 모형은 현재의 관측값을 과거 시점의 값들로 설명하는 모델입니다.AR(1) (현재의 값이 1시점 이전의 값과 연관됨)AR(p) (일반화: 현재의 값이 p시점 이전의 값까지와 연관됨) AR 모델은 다음과 같은 특징을 가집니다.불확실 요소(impact 또는 innovation)는 정규분포를 따른다는 가정을 함계수는 독립적인 상수가 아니라 데이터의 평균과 관련됨모델의 정상성을 판단하려면 특성근(characteristic root)을 구해야 함.p=1일 때, 과거 1시점 이전의 값에 대한 계수의 절댓값이 1이하면 정상성 유지됨이때..

시계열 분석(Time Series Analysis)은 시간의 흐름에 따른 데이터를 다루는 통계 기법으로, 금융, 기후, 마케팅 등 다양한 분야에서 활용되고 있습니다. 이러한 분석을 수행하기 전, 반드시 이해해야 할 개념이 바로 정상성(Stationarity)입니다. 비정상 시계열 (Non-Stationary Time Series)비정상 시계열은 시간이 지남에 따라 확률적 특성이 변하는 시계열을 의미합니다.여기서 확률적 특성이란 평균, 분산, 자기상관계수와 같은 값들을 말합니다.이러한 데이터는 일반적으로 다음과 같은 특징을 가집니다. 평균이 일정하지 않음분산이 시간에 따라 변함시점 간 상관성이 일정하지 않음데이터에 뚜렷한 추세(trend)가 존재함 예) 랜덤 워크(Random Walk)이러한 비정상 시계..