just-data

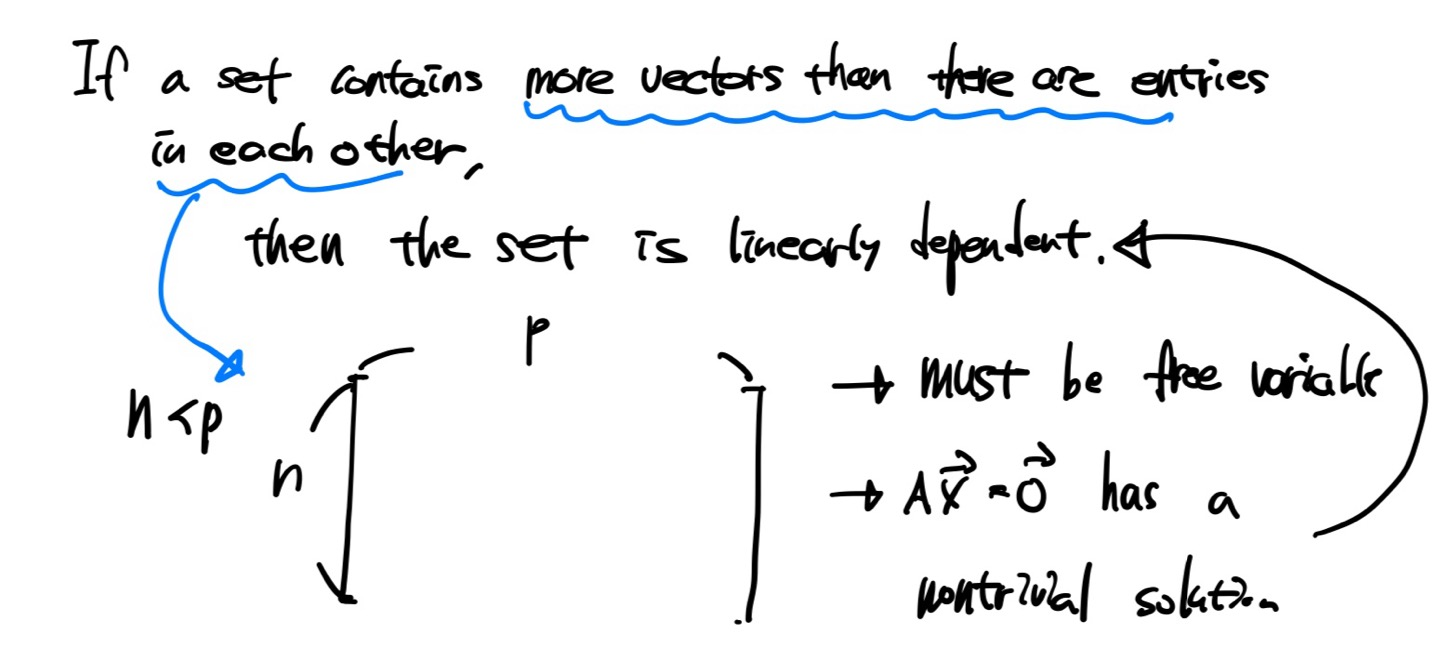
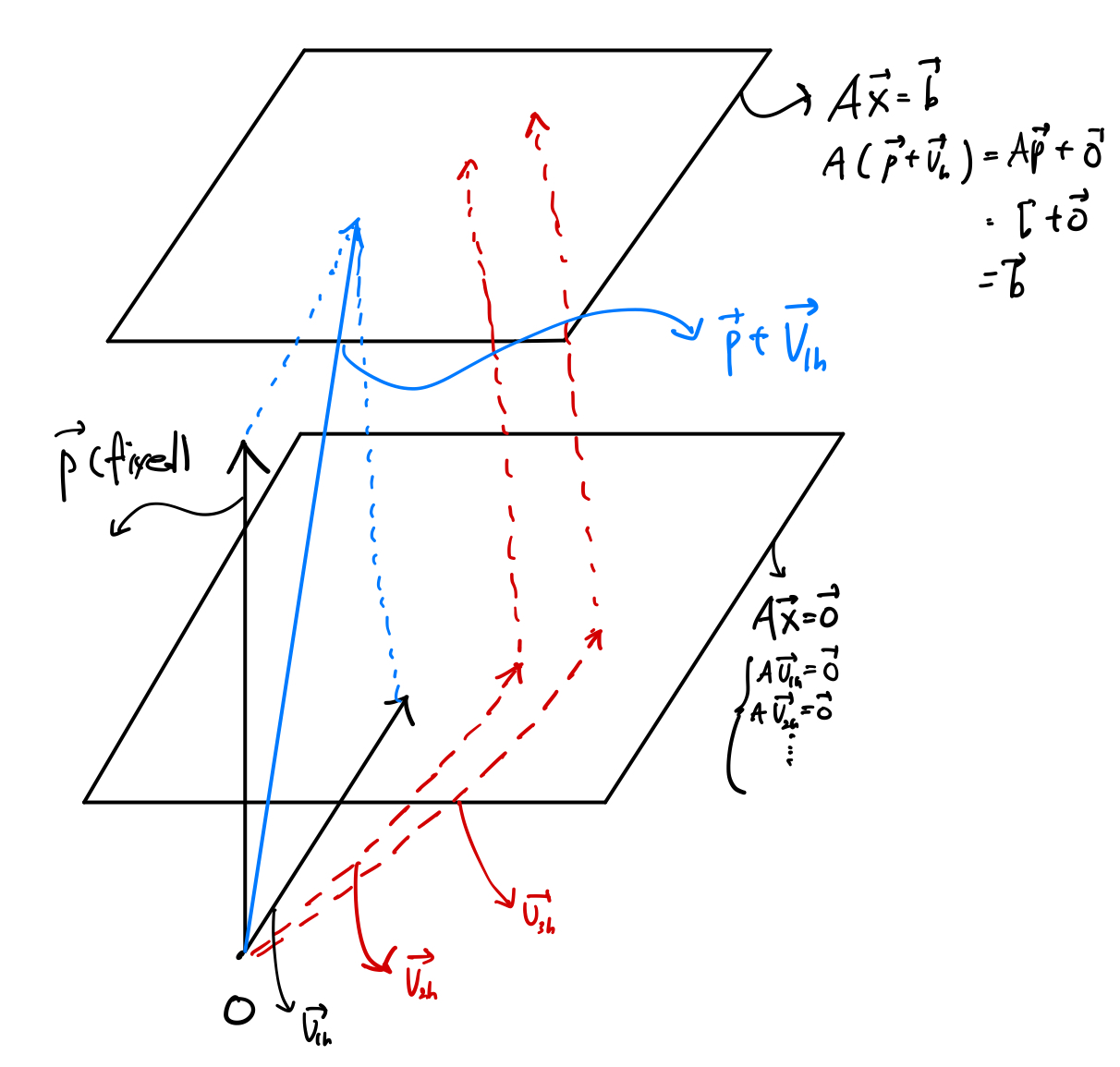
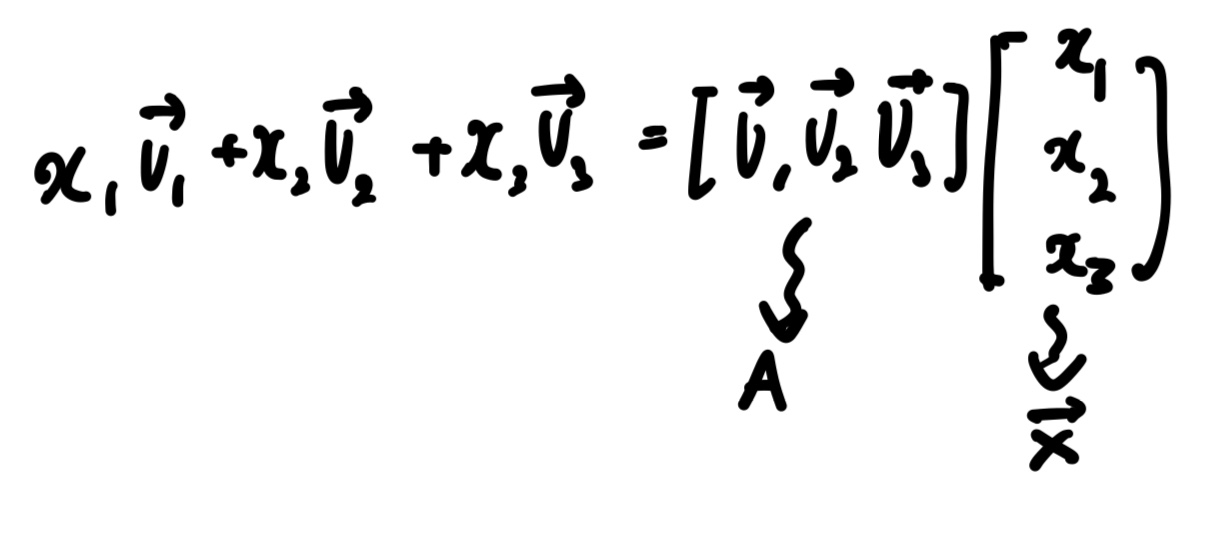이번 글에서는 Inverse matrix의 정의, 존재 조건, 성질, 역행렬 만드는 법을 정리했습니다. 목차 역행렬의 정의 역행렬의 존재 조건 역행렬의 성질 역행렬 만드는 법 1) Elementary Matrices 2) Gauss–Jordan Elimination 3) Adjoint & Determinant 역행렬과 연립방정식 머신러닝/딥러닝에서의 활용 역행렬의 정의 정방행렬 \(A \in \mathbb{R}^{n \times n}\)에 ..

이번 글에서는 대표적인 행렬 유형과 부분·분할(블록) 행렬을 정리하도록 하겠습니다. 목차 대각 행렬 · 영행렬 스칼라 행렬 · 항등 행렬 상·하삼각 행렬 대칭 · 교대 대칭 행렬 부분 행렬 분할(블록) 행렬 Gradient Descent와 분할 계산 대각 행렬 · 영행렬 대각 행렬(diagonal): 주대각선 밖이 모두 0. \[ \begin{bmatrix} 1 & 0 & 0\\ 0 & 2 & 0\\ 0 & 0 & 3 \end{bmatrix} ..

1. 행렬 덧셈 성질같은 크기의 \(m \times n\) 행렬 \(A, B, C\)에 대해:교환법칙: \(A + B = B + A\)결합법칙: \((A + B) + C = A + (B + C)\)항등원과 역원: \(A + O = A,\ \ A + (-A) = O\) (여기서 \(O\)는 영행렬) 2. 행렬 곱셈 성질곱셈이 정의되는 행렬 \(A, B, C\)에 대해:결합법칙: \(A(BC) = (AB)C\)분배법칙(오른쪽): \((A + B)C = AC + BC\)분배법칙(왼쪽): \(C(A + B) = CA + CB\) 3. 실수배, 전치 성질행렬 \(A, B\)와 실수 \(a, b\)에 대해:\((ab)A = a(bA) = b(aA)\)\((a + b)A = aA + bA\)\(a(A + B) = a..

이번 글에서는 행렬(Matrix)과 벡터(Vector), 그리고 이들의 연산과 연립 일차 방정식과의 관계를 다룹니다.1) 행렬 (Matrix)행렬(matrix)은 수를 직사각형 형태로 배열한 것입니다. 일반적으로 \(m \times n\) 행렬은 \(m\)개의 행(row)과 \(n\)개의 열(column)을 갖습니다.\[ A = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{bmatrix} \] 2) 벡터 (Vector)벡터(vector)는 방향과 크기를 가..

선형대수학은 머신러닝 공부에서 가장 기본이 되는 내용입니다. 이 글에서는 방정식과 선형 시스템을 주제로 살펴보도록 하겠습니다.1) 방정식 (Equation)방정식은 두 수식이 서로 같음을 나타냅니다. 보통 미지수 \(x\)를 포함하며, 그 값을 찾아내는 것이 목표입니다.예: \(\;2x + 3 = 7\;\) 에서 이를 만족하는 \(x\)는 \(x=2\)입니다. 즉, 방정식은 주어진 조건을 만족하는 미지수의 값을 찾는 문제입니다. 2) 일차 방정식 (Linear Equation)일차 방정식은 미지수가 1차(제곱 이상의 고차항 없음)로 나타나는 방정식입니다. 일반형은 다음과 같습니다.\[ a_1x_1 + a_2x_2 + \cdots + a_nx_n = b \]\(a_1,\dots,a_n\): 상수(계수)\(..

Matrix Multiplication TransformationA transformation(or function or mapping) &T& from $\mathbb{R}^n$ to $\mathbb{R}^m$ Matrix Transformation Ex.$$ \begin{bmatrix}1&0&0 \\0&1&0 \\0&0&1 \end{bmatrix}=A$$$$ \begin{bmatrix}1&0&0 \\0&1&0 \\0&0&1 \end{bmatrix}\begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix}=\begin{bmatrix}x_1\\x_2\\0\end{bmatrix}$$ Ex.$$\begin{bmatrix}1&3 \\0&1 \end{bmatrix}$$$$\begin{bmatri..

Linearly Independence A set of vectors $\begin{Bmatrix}\mathbf{v}_1 & \mathbf{v}_2&\cdots& \mathbf{v}_p\end{Bmatrix}$ in $\mathbb{R}^n$ is sasid to be linearly independentif the vector equation $x_1\mathbf{v}_1+ x_2\mathbf{v}_2+\cdots + x_p\mathbf{v}_p=\mathbf{0} $ has only the trivial solution  → coefficient가 모두 0인 솔루션만 존재 Linearly DependenceA set of vectors $\begin{Bmatrix}\mathbf{v}_1 & \math..

Homogeneous Linear systems$A\mathbf{X}=\mathbf{0}$ always has at least one solution $\mathbf{X}=\mathbf{0}$. (Trivial Solution) if and only if the equation has at least one free variables(infinitely many solutions): Nontrivial Solution   Ex. Determine whether there is a nontrivial solution.$$\left\{\begin{matrix}3x_1+5x_2-4x_3=0  \\ -3x_1-2x_2+4x_3=0  \\ 6x_1+x-2-8x_3=0 \end{matrix}\right. $$ So..

$A \mathbf{X}$: Product of $A$ and $ \mathbf{X}$ $A$ is $m \times n$, with columnns $\mathbf{a}_1, \mathbf{a}_2, \cdots, \mathbf{a}_n$$$\mathbf{X} \; in \; \mathbb{R}^n$$ $$A\mathbf{X}=[\mathbf{a}_1, \mathbf{a}_2, \cdots, \mathbf{a}_n]\begin{bmatrix}x_1 \\ \vdots\\ x_n \end{bmatrix}=x_1\mathbf{a}_1+x_2\mathbf{a}_2+ \cdots + x_n\mathbf{a}_n$$ → the linear combination of the columns of $A$ using t..

Vectors in $ \mathbb{R}^2$$$\mathbf{u}=\begin{bmatrix}3 \\-1\end{bmatrix} =(3,-1), \mathbf{v}=\begin{bmatrix} 0.2 \\0.3 \end{bmatrix} =(0.2,0.3), \mathbf{w}=\begin{bmatrix} w_1 \\w_2 \end{bmatrix} =(w_1,w_2)$$ ※ vector를 나타내는 기호는 bold로 작성합니다.※ $ \mathbb{R}^2 $: R2 Space Vector Summarization$$\mathbf{u}+\mathbf{v}=\begin{bmatrix}3 \\-1\end{bmatrix}+\begin{bmatrix}0.2 \\0.3\end{bmatrix} =\begin{bma..