[Time Series#3] Box-Cox 변환

시계열 데이터 분석을 진행하다 보면, 원시 데이터의 분포나 분산이 모델링에 적합하지 않은 경우가 많습니다.

특히 예측 모델은 정상성(stationarity)을 기본 전제로 하는 경우가 많기 때문에, 데이터의 분산을 안정화하고 분포를 변환하는 과정이 필요합니다.

 

이때 유용하게 사용되는 대표적인 기법이 바로 박스-콕스(Box-Cox) 변환입니다.

 

출처: https://nachi-keta.medium.com/transforming-data-for-statistical-analysis-the-power-of-box-cox-transformation-a4a059ad2397

 

 

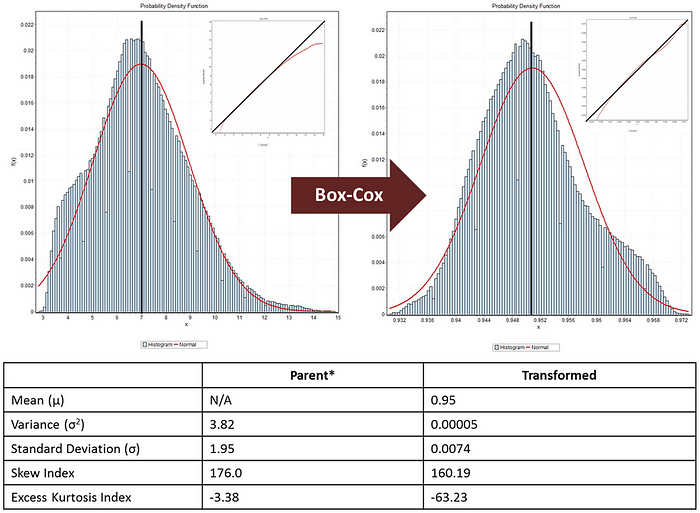
왜 박스-콕스 변환을 사용하는가?

박스-콕스 변환은 시계열 데이터를 모델에 투입하기 전에 사전 처리(preprocessing) 단계에서 적용하는 기법으로, 다음과 같은 효과를 기대할 수 있습니다.

• 변동성 안정화: 데이터의 표준편차를 일정하게 유지하게 함
• 비대칭 분포 개선: 오른쪽 꼬리가 긴 분포를 압축하여 정규성에 가까운 형태로 변환
• 예측 성능 향상: 모델이 더 잘 작동할 수 있는 형태로 데이터를 정제
• 잔차 분석의 안정성: 모델의 잔차가 백색잡음에 가까워지도록 유도

 

 

박스-콕스 변환의 수식과 조건

박스-콕스 변환은 양의 값을 갖는 시계열에만 적용 가능합니다.

만약 데이터에 0 또는 음수가 포함되어 있다면, 먼저 모든 값에 적절한 양의 상수를 더하여 변환 조건을 만족시켜야 합니다.

 

변환은 파라미터 λ값에 따라 아래와 같이 나뉩니다:

• λ = 0

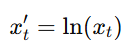
• λ ≠ 0

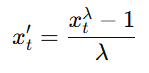
※ λ 값은 보통 로그우도(log-likelihood)를 최소화하는 방식으로 추정됩니다.

 

 

역변환

모델링을 위해 박스-콕스 변환을 적용했다면, 예측 결과를 다시 원래 단위로 복원하기 위해 역변환이 필요합니다.

이 또한 λ 값에 따라 다음과 같이 수행됩니다:

• λ = 0

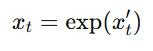
• λ ≠ 0

 

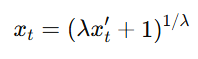
※  만약 변환 전에 양의 상수를 더해주었다면, 역변환 후 반드시 같은 상수를 빼주어야 원래 스케일로 복원할 수 있습니다.

 

 

 

유의 사항

 

• 박스-콕스 변환은 예측의 신뢰구간에 큰 영향을 줄 수 있습니다.
• 평균값은 λ 변화에 크게 영향을 받지 않지만, 분산이나 분포는 민감합니다.
• 정규성을 강제하기보다는, 데이터 특성과 예측 목적에 따라 적용 여부를 판단해야 합니다.