저번 포스팅에서는 thesaurus를 통해 컴퓨터에게 자연어의 의미 전달하는 방법에 대해 알아보았습니다.
2023.05.12 - [Deep Learning] - [NLP#1] 자연어 처리란? - thesaurus
이번 글에서는 저번 시간에 이어서 통계 기반 기법에 대해 알아보도록 하겠습니다.
컴퓨터에게 자연어를 이해시키기 위한 수단으로써 첫 번째로 수작업으로 단어 간 관계를 정의하는 시도가 있었습니다. 대표적인 예로 스탠퍼드에서 만들고 있는 WordNet을 소개해드렸습니다.
하지만 이런 thesaurus는 사람이 직접 관계를 구축하기 때문에 단어의 동적인 요소와 미묘한 차이를 표현할 수 없다는 점과 비용이 많이 든다는 단점이 존재했습니다.
따라서 이를 해결하기 위해 단어의 뜻을 자동으로 추출하는 '통계 기반 기법'을 고안하게 됩니다.
통계 기반 기법
통계 기반 기법부터는 말뭉치 즉, corpus를 통해 단어를 특정 벡터로 표현하게 됩니다.
corpus란 대량의 텍스트 데이터를 의미합니다. 일반 텍스트 데이터와는 달리 자연어 처리를 위해서 수집된 텍스트 데이터를 의미합니다.
이 corpus에 자연어에 대한 사람의 지식이 충분히 담겨있다는 전제로 의미를 추출하게 됩니다. 따라서 어떤 corpus를 데이터로 사용하냐에 따라 단어마다 추출되는 의미가 달라질 수 있습니다.
그래서 어떤 방법을 통해 단어의 의미를 파악할까요? 여기서 분포 가설이라는 중요한 개념이 등장하게 됩니다.
분포가설이란 단어의 의미는 주변 단어(맥락)에 의해 형성된다는 가설입니다.
자연어 처리의 연구는 수업이 이뤄져 왔지만 중요한 기법의 대부분은 이러한 분포 가설에 뿌리를 두고 있습니다.
예를 들어 "I drink beer", "We drink wine" , "I guzzle beer", "We guzzle wine" 이렇게 4개의 문장이 있습니다. 여기서 알 수 있듯이 drink, guzzle 주변에는 음료가 등장하기 쉽다는 것과 두 단어가 가까운 의미의 단어라는 것을 추측할 수 있습니다.
여기서 I, We, wine, beer과 같이 drink와 guzzle를 파악하기 위한 주변 단어들을 context(맥락)이라고 부르도록 하겠습니다. 또한 주변의 몇개의 단어들을 이용하는지를 window size라고 합니다. window size가 2면 아래의 사진처럼 You, say, and, i를 고려하게 됩니다.
※ 상황에 따라 한쪽의 단어들만 사용하기도 합니다.

통계 기반 기법은 어떤 단어에 주목했을 때, 그 주변에 어떤 단어가 몇 번이나 등장하는 지를 세어 집계하는 방법입니다.
지금부터는 코드와 함께 순서대로 진행해보도록 하겠습니다.
1. 동시발생 행렬(co-occurrence matrix)
간단하게 단어의 맥락에 해당하는 단어의 빈도를 세어보겠습니다.
만약 You say goodbye and i say hello라는 문장을 예를 들어보겠습니다. you를 target으로 잡는다고 하면 주변 단어는 say 밖에 없을 것입니다. 따라서 you에 대한 단어의 빈도표는 아래와 같습니다.

이렇게 나타내는 것을 동시발생 행렬이라고 합니다. (여기서는 벡터로 나왔지만 모든 단어들을 표현하게 되면 행렬의 형태로 변하기 때문에 행렬이라는 단어를 사용했습니다.)
이를 코드로 구현해보도록 하겠습니다.
※ 전처리는 코드만 첨부하고 따로 설명하지는 않겠습니다.
import numpy as np
import pandas as pd
def preprocess(text):
text = text.lower()
text = text.replace('.', ' .')
words = text.split(' ')
word_to_id = {}
for word in words:
if word not in word_to_id:
new_id = len(word_to_id)
word_to_id[word] = new_id
id_to_word = {id_: word for word, id_ in word_to_id.items()}
corpus = np.array([word_to_id[word] for word in words])
return corpus, word_to_id, id_to_word
text = 'You say goodbye and 1 say hello.'
corpus, word_to_id, id_to_word = preprocess(text)
def create_co_matrix(corpus, vocab_size, window_size=1):
'''동시발생 행렬 생성
:param corpus: 말뭉치(단어 ID 목록)
:param vocab_size: 단어 수
:param window_size: 윈도우 크기(윈도우 크기가 1이면 타깃 단어 좌우 한 단어씩이 맥락에 포함)
:return: 동시발생 행렬
'''
corpus_size = len(corpus)
co_matrix = np.zeros((vocab_size, vocab_size), dtype=np.int32)
for idx, word_id in enumerate(corpus):
for i in range(1, window_size + 1):
left_idx = idx - i # left window_size
right_idx = idx + i # right window_size
if left_idx >= 0:
left_word_id = corpus[left_idx]
co_matrix[word_id, left_word_id] += 1
if right_idx < corpus_size:
right_word_id = corpus[right_idx]
co_matrix[word_id, right_word_id] += 1
return co_matrix
vocab_size = len(word_to_id)
C = create_co_matrix(corpus, vocab_size)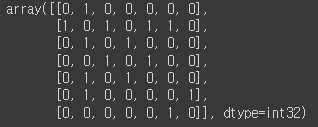
하지만 '발생' 횟수를 사용하는 것은 그리 좋은 방법이 아닙니다.
왜냐하면 모든 문장에 자주 사용되는 the, a, is 등 고빈도 단어가 존재하기 때문입니다.
따라서 이 문제를 해결하기 위해 다른 척도로 수정하도록 하겠습니다.
2. PMI(pointwise mutual information)
PMI는 점별 상호정보량으로써 다음과 같이 정의됩니다.
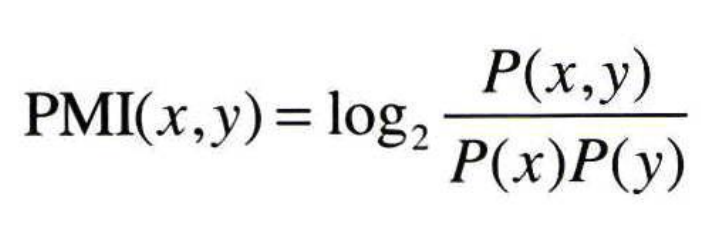
pmi에서는 동시발생 확률을 각 단어의 발생 확률로 나눠주게 됩니다. 즉, 단어가 많이 등장할수록 관련성이 낮아지게 됩니다.
확률이기 때문에 분모는 모두 corpus의 단어 수인데요. 따라서 각 확률마다 전체 단어 수를 곱해주게 되면 아래와 같은 식이 도출되게 됩니다.

pmi가 효과적인지 예를 들어 계산해보겠습니다.
corpus의 단어 수를 10000이라고 하고 the, car, drive를 각각 1000번, 20번, 10번 등장했다고 가정해 봅시다.


계산해 보면 car는 drive와 관련성이 강하도록 도출되게 됩니다.
하지만 만약 동시발생 확률이 0이면(횟수가 0) 마이너스 무한대로 가기 됩니다.
이를 피하기 위해 PPMI(positive PMI)를 사용해 구현해 보도록 하겠습니다.
식은 다음과 같습니다.

def ppmi(C, verbose=False, eps=1e-8):
'''PPMI(점별 상호정보량) 생성
:param C: 동시발생 행렬
:param verbose: 진행 상황을 출력할지 여부
:return: ppmi
'''
M = np.zeros_like(C, dtype=np.float32)
N = np.sum(C) # num of corpus
S = np.sum(C, axis=0) # 각 단어의 출현 횟수
total = C.shape[0] * C.shape[1]
cnt = 0
for i in range(C.shape[0]):
for j in range(C.shape[1]):
pmi = np.log2(C[i, j] * N / (S[i]*S[j]) + eps)
M[i, j] = max(0, pmi)
if verbose:
cnt += 1
if cnt % (total//100) == 0:
print(f'{(100*cnt/total):.2f} 완료')
return M
W = ppmi(C)
PPMI를 통해 우리는 더 좋은 단어 표현을 얻었습니다.
그러나 PPMI 행렬에도 큰 문제가 있습니다. corpus의 단어 수가 증가함에 따라 벡터의 차원의 수도 증가한다는 것입니다. 만약 전체 단어 수가 10만 개라면 벡터의 차원 수도 10만 개가 되게 됩니다.
또한 대부분의 값이 0인 sparse matrix라는 점도 큰 문제입니다. 즉, 중요하지 않은 원소의 수가 대부분을 차지하고 있다는 뜻입니다.
이러한 문제를 해결하기 위해 제시된 방법이 차원 축소입니다.
3. 차원 축소
차원 축소는 중요한 정보는 최대한 유지하면서 벡터의 차원을 줄이는 방법을 의미합니다.
다시말해 데이터를 잘 설명할 수 있는 축을 찾는 일을 의미합니다.

차원 축소를 하는 방법은 여러 가지가 있지만 이번엔 특이값 분해(Singular Value Decomposition, SVD)를 사용해보도록 하겠습니다.

SVD는 임의의 행렬을 세 행렬(U, S, V)의 곱으로 분해하게 됩니다.
이때, U와 V는 직교행렬(orthogonal matrix)이며 S는 대각행렬(diagonal matrix)입니다.
SVD를 통해 도출된 행렬 중 U가 우리가 원하는 행렬입니다.(원래의 행렬과 근사한 행렬)
※ SVD에 대해서는 나중에 자세하게 다루도록 하겠습니다.

이제 파이썬으로 구현해 보도록 하겠습니다.
SVD는 넘파이의 linalg의 svd를 통해 실행할 수 있습니다.
U, S, V = np.linalg.svd(W)
print(U[0])
원래 sparse matrix였던 W 행렬이 dense matrix로 변했다는 것을 알 수 있습니다.
만약 2차원으로 감소시키려면 처음 2열을 사용하시면 됩니다.
2차원으로 축소된 행렬로 단어를 2차원 그래프 상에 나타내보겠습니다.
import matplotlib.pyplot as plt
for word, word_id in word_to_id.items():
plt.annotate(word, (U[word_id, 0], U[word_id, 1]))
plt.scatter(U[:, 0], U[:, 1], alpha=0.5)
plt.show()
그래프가 조금 잘렸지만 goodbye와 hello와 꽤 가까이 위치해 있는 것을 확인할 수 있습니다.
이로써 SVD가 우리가 원하는 결과를 잘 나타낸다는 것을 알 수 있습니다.
하지만 기존 SVD는 전체 행렬을 분해하기 때문에 시간이 오래 걸린다는 단점이 있습니다 이를 위해서 나온 것이 Truncated SVD입니다.
Truncated SVD는 특잇값 즉, S의 대각 성분이 작은 것을 버리는 방식을 사용하여 기존 SVD 보다 빠른 성능을 보이는 기법입니다. sklearn의 radomized_svd에서 사용할 수 있습니다.
from sklearn.utils.extmath import randomized_svd
U, S, V = randomized_svd(W, n_components = 100,
n_iter = 5,
random_state = None)
print(U[0])
import matplotlib.pyplot as plt
for word, word_id in word_to_id.items():
plt.annotate(word, (U[word_id, 0], U[word_id, 1]))
plt.scatter(U[:, 0], U[:, 1], alpha=0.5)
plt.show()
위의 기존 svd와 비슷한 위치를 나타낸 것을 확인할 수 있습니다.
지금까지 배운 것을 다시 정리해 보면 아래와 같은 전개도로 나타낼 수 있습니다.

지금까지 NLP에서 통계 기반 기법에 대해 알아보았습니다.
통계 기반 기법은 분포 가설에 기초하여 특정 단어 근처에 어떤 단어가 몇 번 등장하는지 횟수를 통해 그 의미를 파악하는 기법을 의미합니다. 기존 thesaurus과 다르게 corpus를 이용하여 추출하기 때문에 단어의 뜻을 일일이 입력하지 않아도 된다는 장점이 있습니다.
이번 파이썬 코드에서는 예시 텍스트를 짧은 단어로 예시를 들었습니다. 따라서 자료(corpus의 길이)가 충분하지 않아 단어의 의미를 추출하는데 제약이 있습니다. 또한 SVD와 Truncated SVD의 실행 시간 차이를 체감하지 못했을 겁니다.
직접 실습하실 때는 대량의 corpus를 이용하시면 더 나은 수준의 단어 표현을 얻을 수 있을 것입니다.
다음 시간에는 추론 기반 기법에 대해서 다뤄보도록 하겠습니다.
포스팅 내용중 다른 생각이 있는 분 혹은 수정해야할 부분이 있으시면 댓글을 통해 그 의견을 나눠보면 너무 좋을 것 같습니다.
※ 본 포스팅의 내용은 밑바닥부터 시작하는 딥러닝2를 참고하였습니다.
'NLP' 카테고리의 다른 글
| [LLM#1] What? How? 트랜스포머(Transformer) (6) | 2024.11.15 |
|---|---|
| [NLP#5] LSTM (0) | 2023.07.02 |
| [NLP#4] 순환 신경망(RNN) (0) | 2023.06.28 |
| [NLP#3] 추론 기반(word2vec) (0) | 2023.05.17 |
| [NLP#1] 자연어 처리란? - thesaurus (0) | 2023.05.12 |