$A \mathbf{X}$: Product of $A$ and $ \mathbf{X}$
$A$ is $m \times n$, with columnns $\mathbf{a}_1, \mathbf{a}_2, \cdots, \mathbf{a}_n$
$$\mathbf{X} \; in \; \mathbb{R}^n$$
$$A\mathbf{X}=[\mathbf{a}_1, \mathbf{a}_2, \cdots, \mathbf{a}_n]\begin{bmatrix}x_1 \\ \vdots\\ x_n \end{bmatrix}=x_1\mathbf{a}_1+x_2\mathbf{a}_2+ \cdots + x_n\mathbf{a}_n$$
→ the linear combination of the columns of $A$ using the corresponding entries in $\mathbf{X}$ as weights.
Ex. Matrix Equation
$$\begin{bmatrix}1&2&-1\\0&-5&3\end{bmatrix}\begin{bmatrix}4\\3\\7\end{bmatrix} = 4\begin{bmatrix}1\\0\end{bmatrix}+3\begin{bmatrix}2\\-5\end{bmatrix}+7\begin{bmatrix}-1\\3\end{bmatrix}=\begin{bmatrix}3\\6\end{bmatrix}$$
Ex. Vector equation to matrix equation
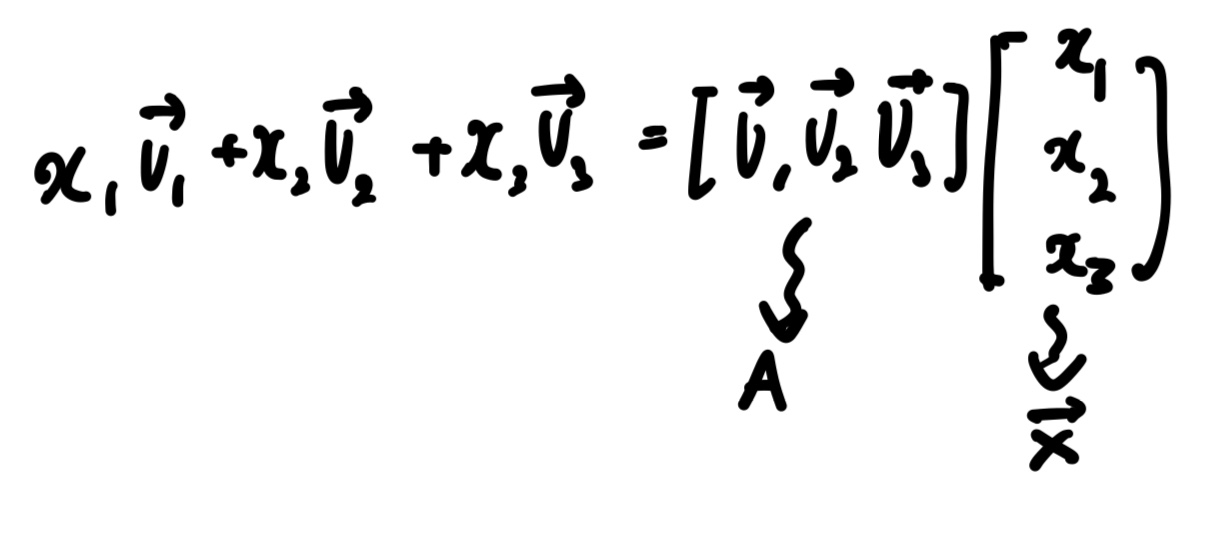
Ex. System of linear equations to matrix equation
$$\left\{\begin{matrix}x_1+2x_2-x_3=4\\-5x_2+3x_3=1\end{matrix}\right.$$
↓
$$x_1\begin{bmatrix}1\\0\end{bmatrix}+x_2\begin{bmatrix}2\\-5\end{bmatrix}+x_3\begin{bmatrix}-1\\3\end{bmatrix}=\begin{bmatrix}4\\1\end{bmatrix}$$
↓
$$\begin{bmatrix}1&2&-1\\0&-5&3\end{bmatrix}\begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix}=\begin{bmatrix}4\\1\end{bmatrix}$$
Ex. More efficient way to compute matrix equation
$$\begin{bmatrix}a_{11}&a_{12}&a_{13}
\\a_{21}&a_{22}&a_{23}
\\a_{31}&a_{32}&a_{33}\end{bmatrix}\begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix}=
\begin{bmatrix}a_{11}x_1+a_{12}x_2+a_{13}x_3
\\ a_{21}x_1+a_{22}x_2+a_{23}x_3
\\ a_{31}x_1+a_{32}x_2+a_{33}x_3
\end{bmatrix} $$
※
$$\begin{bmatrix}1&0&0
\\0&1&0
\\0&0&1\end{bmatrix}\begin{bmatrix}r\\s\\t\end{bmatrix}=
\begin{bmatrix}r&s&t\end{bmatrix} $$
Theorem 3.
$A$ is $m \times n$ matrix, with columns $\mathbf{a}_1, \mathbf{a}_2, \cdots, \mathbf{a}_n$, $\mathbf{b}$ is in $ \mathbb{R}^n $
- Matrix Equation: $A \mathbf{X}=\mathbf{b}$
- Vector Equation: $x_1\mathbf{a}_1+ x_2\mathbf{a}_2 + \cdots + x_n\mathbf{a}_n=\mathbf{b}$
- Augmented Matrix: $[\mathbf{a}_1, \mathbf{a}_2, \cdots, \mathbf{b}]$
have the same solution set
→ some linear systems can be seen as 3 way
Theorem 4.
$A$ is $m \times n$ matrix, with columns $\mathbf{a}_1, \mathbf{a}_2, \cdots, \mathbf{a}_n$
The followings are all true or all false
- For each $\mathbf{b}$ in $\mathbb{R}^m$, $A\mathbf{x} = \mathbf{b}$ has a solution.
- Each $\mathbf{b}$ in $\mathbb{R}^m$ is a linear combination of the columns of $A$.
- The columns of $A$ span $\mathbb{R}^m$
- $A$ has a pivot position in every row.

Theorem 5.
If $A$ is an $m \times n$ matrix, $\mathbf{u}$ and $\mathbf{v}$ are vectors in $\mathbb{R}^n$,
and $c$ is a scalar, then
- $A(\mathbf{u} + \mathbf{v})=A\mathbf{u}+A\mathbf{v}$
- $A(c\mathbf{u})=cA\mathbf{u}$
※ Reference
<선형대수학개론 of 조범희(인프런)>