Vectors in $ \mathbb{R}^2$
$$\mathbf{u}=\begin{bmatrix}3 \\-1\end{bmatrix} =(3,-1), \mathbf{v}=\begin{bmatrix} 0.2 \\0.3 \end{bmatrix} =(0.2,0.3), \mathbf{w}=\begin{bmatrix} w_1 \\w_2 \end{bmatrix} =(w_1,w_2)$$
※ vector를 나타내는 기호는 bold로 작성합니다.
※ $ \mathbb{R}^2 $: R2 Space
Vector Summarization
$$\mathbf{u}+\mathbf{v}=\begin{bmatrix}3 \\-1\end{bmatrix}+\begin{bmatrix}0.2 \\0.3\end{bmatrix} =\begin{bmatrix}3.2 \\-0.7\end{bmatrix}$$
Scalar Multiplication
$$c=5$$
$$c\mathbf{u}=5\begin{bmatrix}3 \\-1\end{bmatrix}=\begin{bmatrix}5\times 0.2 \\5\times0.3 \end{bmatrix} =\begin{bmatrix}15 \\-5 \end{bmatrix}$$
Geometric Description of $ \mathbb{R}^2$
$$\mathbf{u}=\begin{bmatrix}2 \\2\end{bmatrix}, \mathbf{v}=\begin{bmatrix}-6 \\1\end{bmatrix},\mathbf{u}+\mathbf{v}=\begin{bmatrix}-4 \\3\end{bmatrix}$$


Vectors in $ \mathbb{R}^3$
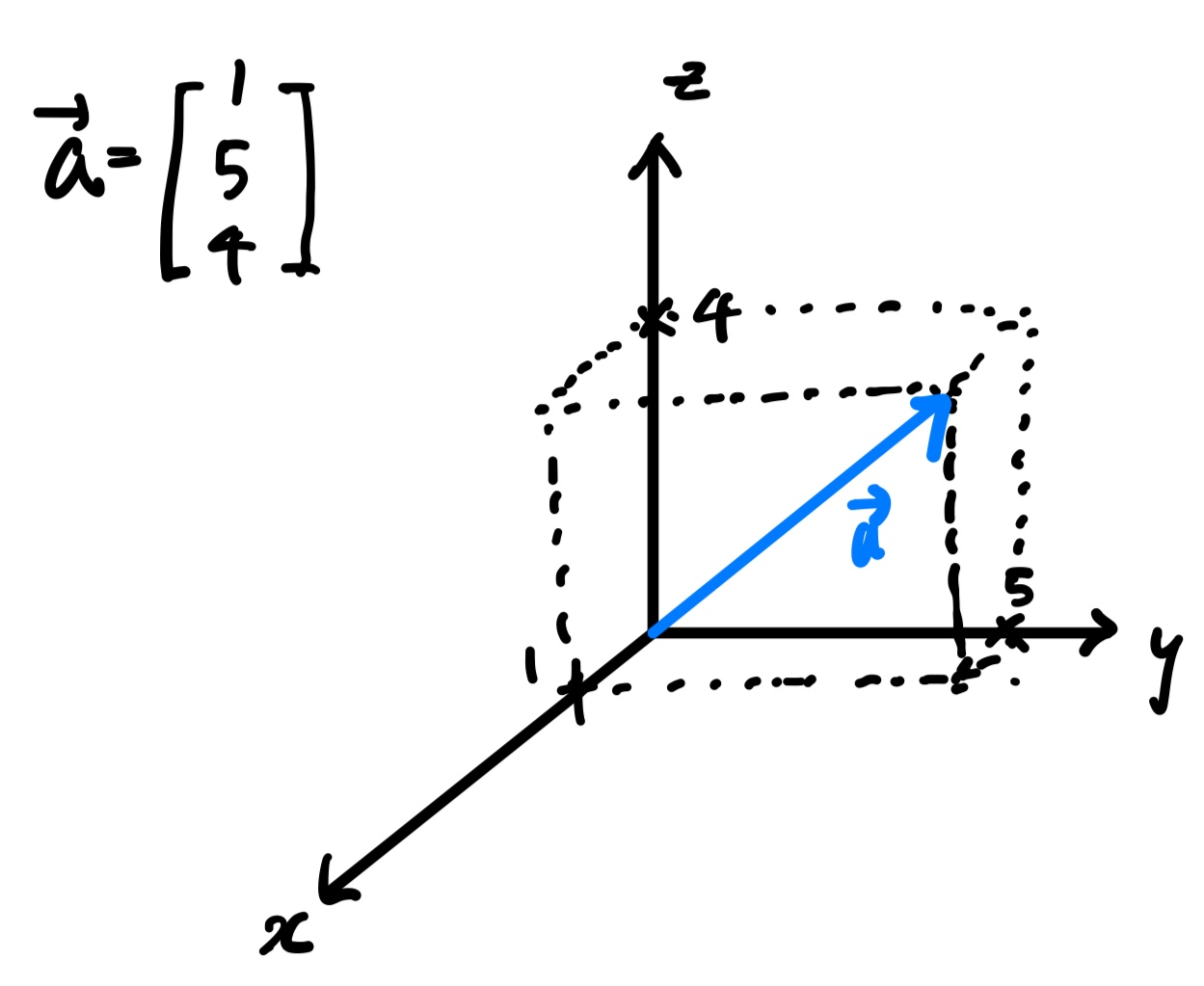
Vectors in $ \mathbb{R}^n$
$$\mathbf{u}=\begin{bmatrix}u_1
\\u_2
\\\vdots
\\u_n
\end{bmatrix}=(u_1, u_2,\cdots ,u_n)$$
Algebraic properties of $ \mathbb{R}^n$
$$ \mathbf{u} , \mathbf{v}, \mathbf{w} \; in \; \mathbb{R}^n $$
$$ c,d: scalar $$
- $ \mathbf{u} + \mathbf{v}= \mathbf{v}+ \mathbf{u} $
- $ (\mathbf{u}+ \mathbf{v})+ \mathbf{w}= \mathbf{u}+( \mathbf{v}+ \mathbf{w})$
- $ \mathbf{u}+ \mathbf{0}= \mathbf{0}+ \mathbf{u}= \mathbf{u}$
- $ \mathbf{u}+(-\mathbf{u})= (-\mathbf{u})+\mathbf{u}=\mathbf{0}$
- $c(\mathbf{u}+\mathbf{v})=c\mathbf{u}+c\mathbf{v}$
- $(c+d) \mathbf{u} =c \mathbf{u} +d \mathbf{u} $
- $c(d \mathbf{u})=(cd) \mathbf{u}$
- $1 \mathbf{u}= \mathbf{u}$
※ How to prove?
Ex.
$$\mathbf{u}=\begin{bmatrix}a \\b\end{bmatrix},\mathbf{v}=\begin{bmatrix}c \\d\end{bmatrix}$$
$$\mathbf{u}+\mathbf{v}=\begin{bmatrix}a+c \\b+d\end{bmatrix}=\begin{bmatrix}c+a \\d+b\end{bmatrix}=\mathbf{v}+\mathbf{u}$$
Linear Combinations
$$ \mathbf{v}_1, \mathbf{v}_2, \cdots, \mathbf{v}_p \; in \; \mathbb{R}^n $$
$$c_1, c_2, \cdots, c_p: Scalar$$
$$ \mathbf{y} = c_1 \mathbf{v}_1+ c_2 \mathbf{v}_2+ \cdots+ c_p \mathbf{v}_p $$
Ex 1. Can $ \mathbf{b} $ be generated as a linear combination of $a_1$ and $a_2$?
$$ \mathbf{a}_1=\begin{bmatrix}1\\-2\\5\end{bmatrix}, \mathbf{a}_2=\begin{bmatrix}2\\5\\6\end{bmatrix}, \mathbf{b}=\begin{bmatrix}7\\4\\3\end{bmatrix}$$
Sol)

A vetor equation
$ x_1 \mathbf{a}_1 + x_2 \mathbf{a}_2+ \cdots+ x_n \mathbf{a}_n = \mathbf{b} $ has the same solution set the linear system whose augmented matrix is $\begin{bmatrix}a_1 & a_2 & \cdots & a_n & b \\ \end{bmatrix}$
→vector equation과 augmented matrix가 서로 긴밀한 관계가 있다.
$Span\begin{Bmatrix} \mathbf{v}_1, & \mathbf{v}_2, & \cdots, & \mathbf{v}_p \\ \end{Bmatrix}$ is the collection of all vectors that can be written in the form
$$ c_1 \mathbf{v}_1 + c_2 \mathbf{v}_2+ \cdots+ c_p \mathbf{v}_p $$
※ $\mathbf{v}_1, \mathbf{v}_2, \cdots, \mathbf{v}_p $를 Span 했다.
Ex. Is a vector $b$ in $Span\begin{Bmatrix} \mathbf{v}_1, & \mathbf{v}_2, & \cdots, & \mathbf{v}_p \\ \end{Bmatrix}$?
= Does the following vector equation have a solution?
$$ x_1 \mathbf{v}_1 + x_2 \mathbf{v}_2+ \cdots+ x_n \mathbf{v}_n = \mathbf{b} $$
= Does the following augmented matrix have a solution?
$$ \begin{bmatrix} \mathbf{v}_1 & \mathbf{v}_2 & \cdots & \mathbf{b} \\ \end{bmatrix} $$
Geometric descriptions of $Span\begin{Bmatrix} \mathbf{v}\\ \end{Bmatrix}$ and $Span\begin{Bmatrix} \mathbf{u}, & \mathbf{v} \\ \end{Bmatrix}$ in $ \mathbb{R}^3$

※ Reference
<선형대수학개론 of 조범희(인프런)>