Homogeneous Linear systems
$A\mathbf{X}=\mathbf{0}$ always has at least one solution $\mathbf{X}=\mathbf{0}$. (Trivial Solution)
if and only if the equation has at least one free variables(infinitely many solutions): Nontrivial Solution
Ex. Determine whether there is a nontrivial solution.
$$\left\{\begin{matrix}3x_1+5x_2-4x_3=0
\\ -3x_1-2x_2+4x_3=0
\\ 6x_1+x-2-8x_3=0
\end{matrix}\right. $$
Sol)
$$\begin{bmatrix}3&5&-4&0
\\ -3&-2&-4&0
\\ 6&1&-8&0
\end{bmatrix}\sim
\begin{bmatrix}1&0&-4/3&0
\\0&1&0&0
\\0&0&0&0
\end{bmatrix} $$
$$\left\{\begin{matrix} x_1=4/3x_3
\\ x_2=0
\\x_3\;is\;free
\end{matrix}\right.$$
↓
$$\mathbf{X}=\begin{bmatrix}4/3x_3
\\0
\\x_3
\end{bmatrix}=x_3\begin{bmatrix}4/3\\0\\1\end{bmatrix}=x_3\mathbf{V},\;where\;\mathbf{V}=\begin{bmatrix}4/3\\0\\1\end{bmatrix}$$
↓
$$Span\begin{Bmatrix}\mathbf{V}\end{Bmatrix}$$→line
Ex. Determine whether there is a nontrivial solution.
$$10x_1-3x_2-2x_3=0$$
$$\mathbf{X}=\begin{bmatrix}0.3x_2+0.2x_3
\\x_2
\\x_3
\end{bmatrix}=
\begin{bmatrix}
0.3x_2
\\x_2
\\0\end{bmatrix}+
\begin{bmatrix}0.2x_3
\\0
\\x_3
\end{bmatrix} $$
$$=x_2\begin{bmatrix}0.3\\1\\0\end{bmatrix}+x_3\begin{bmatrix}0.2\\0\\1\end{bmatrix}$$
$$=x_2\mathbf{u}+x_3\mathbf{v},\;where\;\mathbf{u}=\begin{bmatrix}0.3\\1\\0\end{bmatrix},\;\mathbf{
v}=\begin{bmatrix}0.2\\0\\1\end{bmatrix}$$
↓
$$Span\begin{Bmatrix}\mathbf{u}&\mathbf{v}\end{Bmatrix}$$
→ plane
▶ The solution set of $A\mathbf{X}=\mathbf{0}$ can always expressed as $Span\begin{bmatrix}\mathbf{v}_1 & \mathbf{v}_1 & \cdots & \mathbf{v}_p \end{bmatrix}$
※ tirivial solution: $Span\begin{bmatrix}\mathbf{0}\end{bmatrix}$
Nonhomogeneous Linear Systems
$A\mathbf{X}=\mathbf{b}$
Ex. Describe all solutions
$$A\mathbf{X}=\mathbf{b},\;A=\begin{bmatrix}5&5&-4
\\ -3&-2&4
\\ 6&1&8
\end{bmatrix},\;\mathbf{b}=\begin{bmatrix}7\\-1\\4\end{bmatrix}$$
$$\begin{bmatrix}5&5&-4&7
\\ -3&-2&4&-1
\\ 6&1&8&4
\end{bmatrix} \sim \begin{bmatrix}1&0&-4/3&-1
\\ 0&1&0&2
\\ 0&0&0&0
\end{bmatrix} $$
$$\mathbf{X}=\begin{bmatrix}4/3x_3-1\\2\\x_3\end{bmatrix}=\begin{bmatrix}-1\\2\\0\end{bmatrix}+
\begin{bmatrix}4/3x_3\\0\\x_3\end{bmatrix}=\begin{bmatrix}-1\\2\\0\end{bmatrix}+x_3\begin{bmatrix}4/3\\0\\1\end{bmatrix} $$
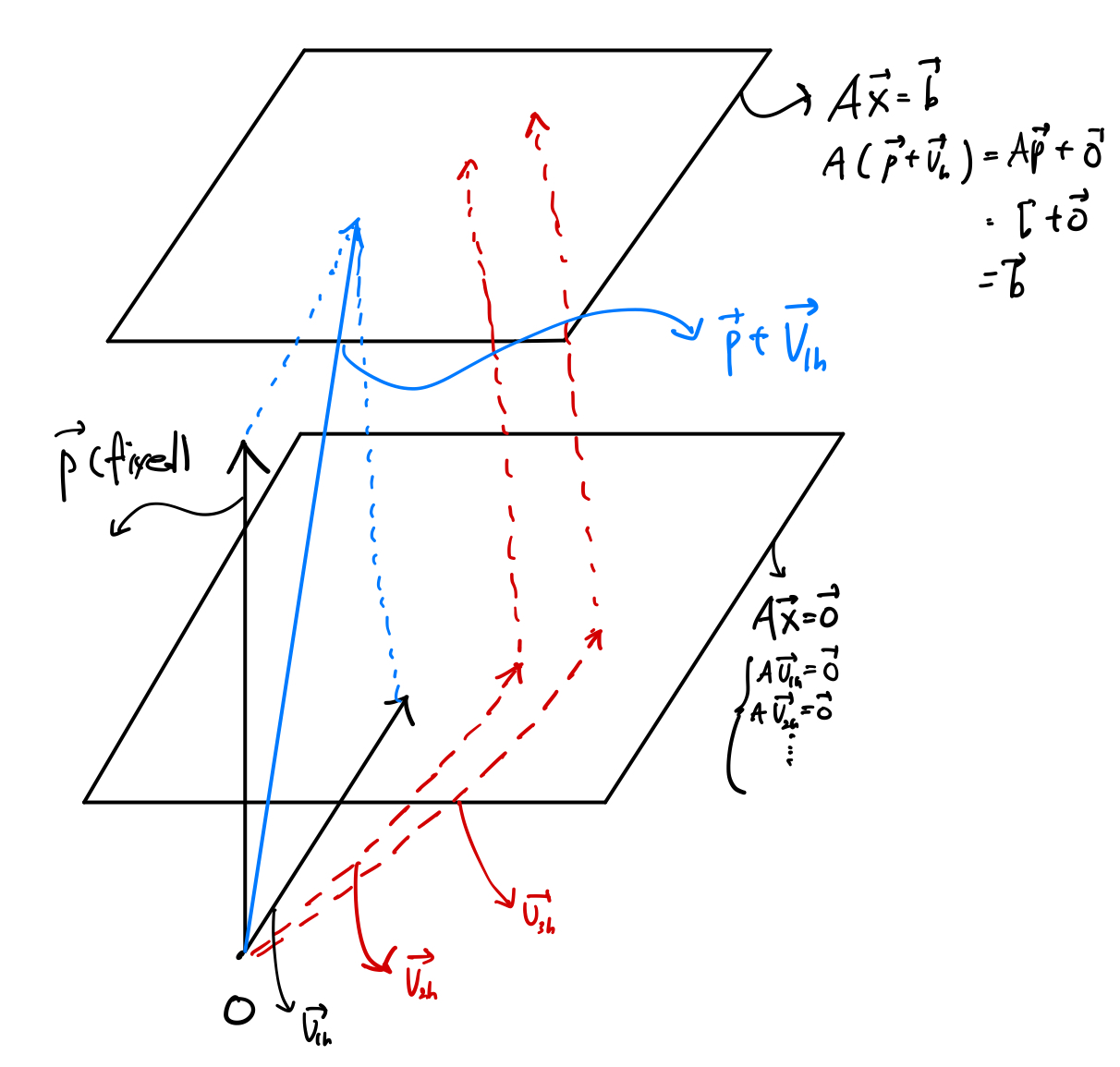
$$=\mathbf{p}+t\mathbf{v}$$
= particular solution(fixed vector) + homogeneous solution
→ homogeneous system과 nonhomogeneous system과 밀접한 관련성이 존재함
Theorem 6.
Suppose
$A\mathbf{X}=\mathbf{b}$ is consistent and let $\mathbf{p}$ be a solution.
Then, the solution set of $A\mathbf{X}=\mathbf{b}$ is the set of all vectors of the form
$$\mathbf{w}=\mathbf{p}+\mathbf{v}_h$$
where $\mathbf{v}_h$ is any solution of the homogeneous eqation $A\mathbf{X}=\mathbf{0}$.
Ex. Understanding Theorem 6 in $\mathbb{R}^3$
※ Reference
<선형대수학개론 of 조범희(인프런)>