[Mathematics#7] Introduction of Linear Transformation (Linear Equations in Linear Algebra#7)

Matrix Multiplication

 

Transformation

A transformation(or function or mapping) &T& from $\mathbb{R}^n$ to $\mathbb{R}^m$

 

Matrix Transformation

 

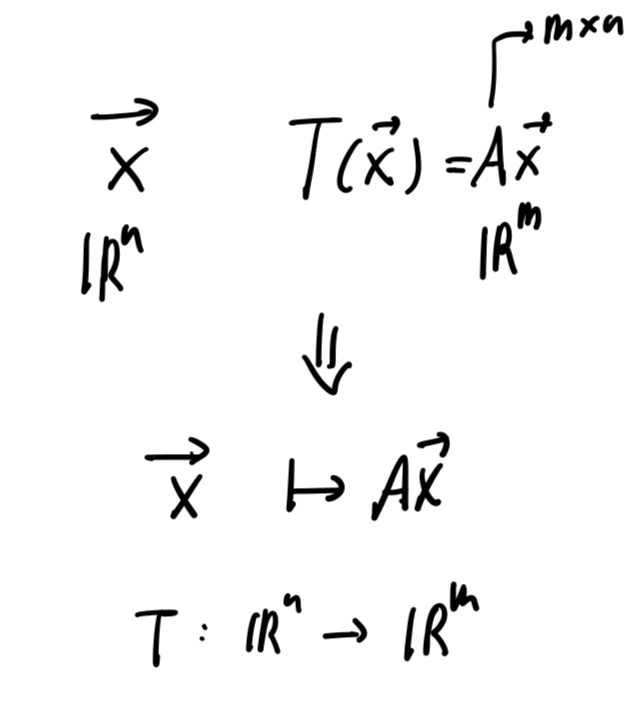
Ex.

$$ \begin{bmatrix}1&0&0
\\0&1&0
\\0&0&1
\end{bmatrix}=A$$

$$ \begin{bmatrix}1&0&0
\\0&1&0
\\0&0&1
\end{bmatrix}\begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix}=\begin{bmatrix}x_1\\x_2\\0\end{bmatrix}$$

 

Ex.

$$\begin{bmatrix}1&3
\\0&1
\end{bmatrix}$$

$$\begin{bmatrix}1&3
\\0&1
\end{bmatrix}\begin{bmatrix}0\\2\end{bmatrix}=\begin{bmatrix}6\\2\end{bmatrix}$$

$$\begin{bmatrix}1&3
\\0&1
\end{bmatrix}\begin{bmatrix}2\\2\end{bmatrix}=\begin{bmatrix}8\\2\end{bmatrix}$$

Linear Transformation

A transformation(or mapping) $T$ is linear if 

$$T(\mathbf{u}+\mathbf{v})=T(\mathbf{u})+T(\mathbf{v})$$

$$T(c\mathbf{u})=cT(\mathbf{u})$$

 

Every matrix transformation is a linear transformation

 

 

 

 

 

 

※ Reference

<선형대수학개론 of 조범희(인프런)>