[Mathematics#1] Systems of Linear Equations (Linear Equations in Linear Algebra#1)

A linear equations in the variables $x_1, x_2, ..., x_n$ should be of below form.

 

$$a_1x_1 + a_2x_2 + ... + a_nx_n = b$$

A System of linear equations(=linear system)

: a collention of one or more linear equations.

$$x_1-2x_2=1$$

$$-x_1+3x_2=3$$

 

Solution set

: The set of all possible solutions of the linear system.

→ Two linear systems are called Equivalent if they have the same solution set.

 

A system of linear equations has either

1. no solution → inconsistent 
2. exactly one solution → consistent
3. infinitely many solutions → consistent

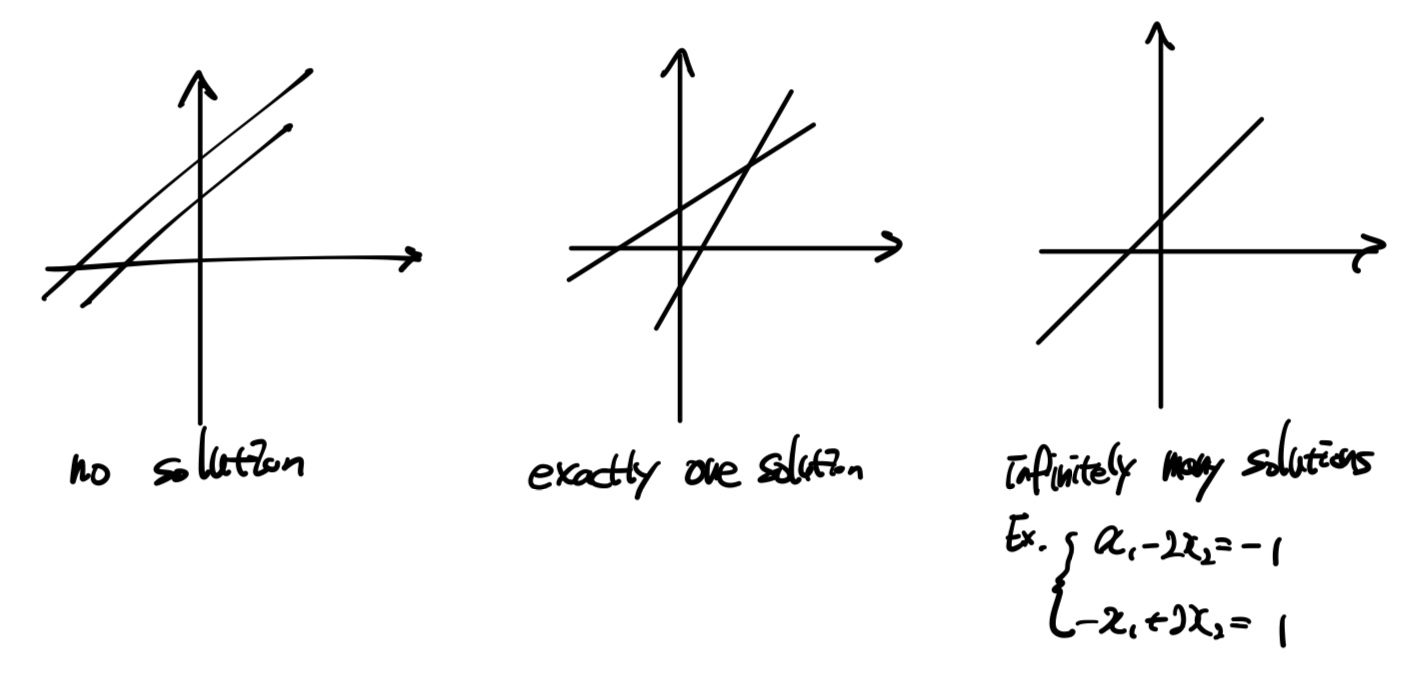
Matrix Notation

Elementary row operations

1. replacement
2. interchange
3. scaling

Ex 1. Solve the follwing systme of linear equations.

$$x_1-2x_2+x_3=0$$

$$2x_2-8x_3=8$$

$$-4x_1+5x_2+9x_3=-9$$

 

Sol)

 

Ex 2. Solve the following system of linear equations.

$$x_2-4x_3=8$$

$$2x_1-3x_2+2x_3=1$$

$$5x_1-8x_2+7x_3=1$$

 

Sol)

We say two matrices are row equivalent if there is a sequence of elementary row operations that transforms one matrix into the other.

 

If the augemented matrices of two linear systems are row equivalent, then two systems have the same solutions.

 

 

 

 

 

 

 

 

 

 

※ Reference

<선형대수학개론 of 조범희(인프런)>