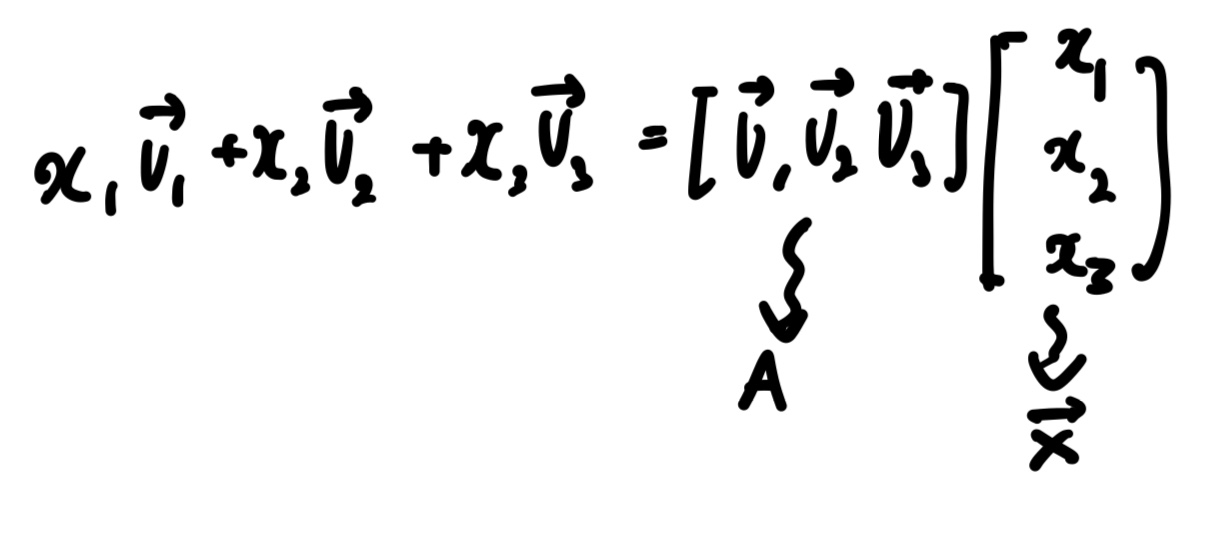just-data

Matrix Multiplication TransformationA transformation(or function or mapping) &T& from $\mathbb{R}^n$ to $\mathbb{R}^m$ Matrix Transformation Ex.$$ \begin{bmatrix}1&0&0 \\0&1&0 \\0&0&1 \end{bmatrix}=A$$$$ \begin{bmatrix}1&0&0 \\0&1&0 \\0&0&1 \end{bmatrix}\begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix}=\begin{bmatrix}x_1\\x_2\\0\end{bmatrix}$$ Ex.$$\begin{bmatrix}1&3 \\0&1 \end{bmatrix}$$$$\begin{bmatri..

Linearly Independence A set of vectors $\begin{Bmatrix}\mathbf{v}_1 & \mathbf{v}_2&\cdots& \mathbf{v}_p\end{Bmatrix}$ in $\mathbb{R}^n$ is sasid to be linearly independentif the vector equation $x_1\mathbf{v}_1+ x_2\mathbf{v}_2+\cdots + x_p\mathbf{v}_p=\mathbf{0} $ has only the trivial solution  → coefficient가 모두 0인 솔루션만 존재 Linearly DependenceA set of vectors $\begin{Bmatrix}\mathbf{v}_1 & \math..

Homogeneous Linear systems$A\mathbf{X}=\mathbf{0}$ always has at least one solution $\mathbf{X}=\mathbf{0}$. (Trivial Solution) if and only if the equation has at least one free variables(infinitely many solutions): Nontrivial Solution   Ex. Determine whether there is a nontrivial solution.$$\left\{\begin{matrix}3x_1+5x_2-4x_3=0  \\ -3x_1-2x_2+4x_3=0  \\ 6x_1+x-2-8x_3=0 \end{matrix}\right. $$ So..

$A \mathbf{X}$: Product of $A$ and $ \mathbf{X}$ $A$ is $m \times n$, with columnns $\mathbf{a}_1, \mathbf{a}_2, \cdots, \mathbf{a}_n$$$\mathbf{X} \; in \; \mathbb{R}^n$$ $$A\mathbf{X}=[\mathbf{a}_1, \mathbf{a}_2, \cdots, \mathbf{a}_n]\begin{bmatrix}x_1 \\ \vdots\\ x_n \end{bmatrix}=x_1\mathbf{a}_1+x_2\mathbf{a}_2+ \cdots + x_n\mathbf{a}_n$$ → the linear combination of the columns of $A$ using t..

Vectors in $ \mathbb{R}^2$$$\mathbf{u}=\begin{bmatrix}3 \\-1\end{bmatrix} =(3,-1), \mathbf{v}=\begin{bmatrix} 0.2 \\0.3 \end{bmatrix} =(0.2,0.3), \mathbf{w}=\begin{bmatrix} w_1 \\w_2 \end{bmatrix} =(w_1,w_2)$$ ※ vector를 나타내는 기호는 bold로 작성합니다.※ $ \mathbb{R}^2 $: R2 Space Vector Summarization$$\mathbf{u}+\mathbf{v}=\begin{bmatrix}3 \\-1\end{bmatrix}+\begin{bmatrix}0.2 \\0.3\end{bmatrix} =\begin{bma..

A nonzero row or columnA leading entry of row: the leftmost nonzero entry※ entry: values in matrixEchelon FormsAll nonzero rows are above any row of all zeros.Each leading entry of a row is in a column to the right of the leading entry of the row above itReduced echelon formsThe leading entry in each nonzero row is 1.Each leading 1 is the only non zero entry in its column.Theorem 1. Uniqueness o..

A linear equations in the variables $x_1, x_2, ..., x_n$ should be of below form. $$a_1x_1 + a_2x_2 + ... + a_nx_n = b$$A System of linear equations(=linear system): a collention of one or more linear equations.$$x_1-2x_2=1$$$$-x_1+3x_2=3$$ Solution set: The set of all possible solutions of the linear system.→ Two linear systems are called Equivalent if they have the same solution set. A system ..